Один из способов количественной оценки риска – это расчет показателей вариации, которые дают представление о том, как отдельные значения результативных показателей (аналогично для показателей эффективности для инвестиционного проекта) группируются вокруг среднего значения (насколько они отдалены от средней величины). Вариация показателя – количественное различие индивидуальных значений этого показателя, полученных при различных сценариях реализации проекта. Чем выше рассеивание результативных показателей (показателей эффективности) вокруг средней величины, тем значительнее степень риска.
По существу, колебания показателя можно определить специальными показателями вариации. Выделяют следующие абсолютные показатели вариации признака:
1) размах вариации, определяемый как разность между наибольшим и наименьшим значениями показателя:
R = xmax — xmin
где хmах – наибольшее значение показателя;
хмin – наименьшее значение показателя;
2) среднее линейное отклонение , которое определяется как средняя арифметическая из абсолютных по модулю отклонений индивидуальных значений от средней:
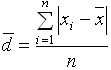
где – среднее значение показателя;
3) дисперсия (s2 – средний квадрат отклонений), определяется как средняя (базовая величина) из отклонений, возведенных в квадрат :
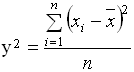
4) среднее квадратическое отклонение – корень квадратный из дисперсии:
![]()
Помимо абсолютных показателей вариации показателя эффективности используют относительные показатели вариации, которые рассчитываются как отношение абсолютного показателя рассеивания к среднему значению, умноженному на 100 %.
Относительные показатели вариации признака:
- коэффициент осцилляции отражает относительную вариацию крайних значений признака вокруг средней:
![]()
- относительное линейное отклонение характеризует долю усредненного значения абсолютных отклонений от средней величины:
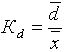
- коэффициент вариации как отношение среднее квадратичного отклонения к среднему значению:
![]()
Если u больше 0,33, то говорят о большой вариации признака в изучаемой совокупности.
