Модель стратегической игры используется для выбора оптимального инвестиционного проекта в случае полной неопределенности. Полная (безнадежная) неопределенность означает отсутствие какой-либо информации о вероятностях реализации сценария развития будущего.
Стратегическая игра – упрощенная формализованная модель реальной ситуации («игры»), в которой участвуют несколько сторон – участников игры (игроков).
Стратегия игрока – их действия в каждой из возможных ситуаций, которые задаются значениями для первого игрока Xi, для второго игрока Yj. Значения zij определяют результат от реализации стратегий двумя игроками и задаются матрицей Z=||zij||, которую называют платежной.
В качестве разновидности модели стратегической игры рассматривают модель стратегической игры с «природой» (внешней средой). Внешняя среда («природа») представляет совокупность внешних факторов, оказывающих влияние на первого игрока. Особенность теории игры с «природой» заключается в том, что в ней сознательно действует только один из участников – первый игрок.
Природа (второй игрок) сознательно против первого игрока не действует, а выступает как партнер, не имеющий конечной цели и случайно осуществляющий ходы. Стратегическая игра задается в виде матрицы А = ||аij||.
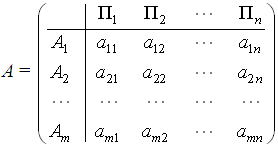
Матрица игры с «природой» задает результат (аij), который получает первый игрок при реализации одной из своих стратегий (А>i) и при некотором состоянии (стратегии) «природы» (Пj). Так как предполагается полная неопределенность в отношении будущего, то вероятности выбора той или иной стратегии «природы» (ее состояния) в этой модели не задаются.
Другой способ задания матрицы игры с внешней средой – задание матрицы рисков R.
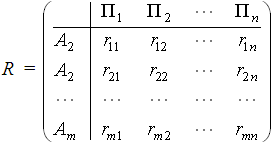
Величина риска – это размер платы за отсутствие информации о состоянии среды. Матрица рисков R=||rij|| строится на основе матрицы А.
Величина риска первого игрока при использовании им стратегии (Аi) и при состоянии внешней среды (Пj) будет разностью между результатом, который получил бы первый игрок, если бы знал, какое состояние внешней среды осуществится (bj), и выигрышем, который первый игрок получит, не имея этой информации (аij):
rij = bj — aij
где bij = max аij в матрице А при заданном j.
Модель стратегической игры с «природой» может быть использована при выборе оптимального инвестиционного проекта. В этом случае в качестве стратегий игрока рассматривают различные сопоставимые инвестиционные проекты, а состояния «природы» интерпретируют как сценарии будущего, которым соответствуют показатели эффективности для каждого проекта. В условиях полной неопределенности заранее неизвестна вероятность реализации того или иного сценария, а значит, и вероятность получения экономического эффекта.
Другими словами, каждый элемент этой матрицы представляет собой показатель эффективности (результат), который имеет место при i-м варианте инвестиций и j-м сценарии развития событий.
Платежная матрица и матрица рисков позволяют выбрать оптимальный инвестиционный проект из набора проектов в платежной матрице с помощью следующих критериев:
1) критерий максимакса:
то есть выбирается тот проект, у которого наибольший экономический эффект во всей платежной матрице. Для этого сначала находят максимальное значение по столбцам платежной матрицы, а затем выбирают максимальное число из выбранных значений;
2) критерий Вальда (максиминный критерий):
то есть выбирается тот проект, у которого наибольший экономический эффект из минимально возможных для каждого проекта. Для этого сначала находят минимальное значение по столбцам платежной матрицы, а затем выбирают максимальное число из выбранных значений;
3) критерий Сэвиджа (критерий минимального риска):
то есть выбирается тот проект, у которого наименьший риск из максимально возможных значений риска для каждого проекта. Для этого сначала находят максимальное значение по столбцам матрицы рисков, а затем выбирают минимальное число из выбранных значений;
4) критерий Гурвица (критерий оптимизма-пессимизма):
где р – коэффициент пессимизма (0 < р < 1).
При выборе оптимального проекта рассчитывают некоторое среднее значение, характеризующее состояние между крайним пессимизмом и «безудержным» оптимизмом. При р = 0 критерий Гурвица совпадает с максимаксным критерием, а при р = 1 совпадает с критерием Вальда.
Если известны вероятности состояний «природы» (осуществления сценариев будущего), то в этом случае имеется только частичная неопределенность, и для выбора оптимального проекта можно использовать обобщающие характеристики случайных величин: математическое ожидание и дисперсию. Расчет математического ожидания позволит определить ожидаемые значения показателей эффективности по каждому варианту инвестиционных проектов, а дисперсия – риск реализации соответствующего инвестиционного проекта.
В частности, оптимальным будет считаться тот проект (в том числе и с точки зрения величины риска), у которого математическое ожидание интегрального эффекта будет наибольшим, а дисперсия этого показателя будет наименьшей.
