Модель экономического роста Солоу — неоклассическая модель экономического роста, выявляющая механизм влияния сбережений, роста трудовых ресурсов и научно-технического прогресса на уровень жизни населения и его динамику.
Модель была разработана в 1956 г. и является простой целью, поскольку представлены только домохозяйства и фирмы.
Р. Солоу в своей модели использовал следующие предпосылки неоклассической экономической школы: совершенная конкуренция, гибкость цен, полная занятость, взаимозаменяемость ресурсов производства, убывающая производительность капитала, постоянная отдача от масштаба, постоянная норма выбытия, отсутствие инвестиционных лагов.
В модели Солоу используется производственная функция Кобба—Дугласа, где труд и капитал являются субститутами. Необходимым условием равновесного состояния экономической системы выступает равенство совокупного спроса и совокупного предложения.
Модель Солоу состоит из следующих уравнений, характеризующих экономическую динамику.
1. Объем предложения на рынке благ описывается производственной функцией с постоянной отдачей от масштаба:
Yt = F(Kt, Lt)
для любого положительного Z верно:
Z Yt = F (ZКt, ZLt)
Предположим, что , тогда получим:
Yt/Lt = F(Kt/Zt,1), (3)
где Yt/Lt — производительность (у); Kt/Zt — капиталовооруженность (фондовооруженность) (k).
Уравнение (3) показывает, что объем производства в расчете на одного работника является функцией капитала на одного работника.
Перепишем исходную функцию:
у = f(k) (4)
На рисунке показана взаимосвязь между производительностью труда и капиталовооруженностью (фондовооруженностью).
Тангенс угла наклона данной производственной функции соответствует предельному продукту капитала (МРК), убывающему по мере роста капиталовооруженности (k).
2. В модели Солоу представлен спрос на товары, предъявляемый со стороны потребителей и инвесторов, т. е. между частным сектором без государственного заказа и чистого экспорта:
Yta= С + I, (5)
тогда it = — инвестиции на одного работника; сt = потребление на одного работника. в модели Солоу
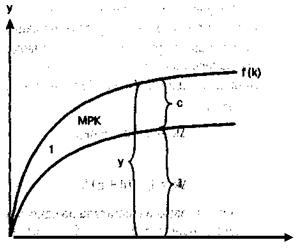
Взаимосвязь между производительностью и капиталовооруженностью (фондовооруженностью)
3. Условием равновесия выступает равенство I и S.
Потребление можно представить:
Сt = (l – S)yt (6)
где норма сбережения (накопления).
Следовательно,
у t = с t + it = (l – S)yt + it (7)
Отсюда:
i = Cy (8)
В условиях равновесия инвестиции равны сбережениям и пропорциональны доходу.
4. Население страны увеличивается постоянным темпом:
Rt = R0(l + n)t, (9)
где n — постоянный темп увеличения населения.
5. В экономике благодаря гибкости цен на рынке факторов производств поддерживается постоянно полная занятость, т. е. численность занятых растет тем же темпом, что и численность населения в стране:
Lt = L0(l + n)t (10)
Запасы капитала могут изменяться, если:
- инвестиции приводят к росту запасов капитала;
- часть капитала амортизируется, что приводит к уменьшению запасов капитала;
- часть капитала идет на вновь вовлекаемых работников.
Таким образом:
Δkt = i t — dkt — n k t,
или
Δk t = i t – (d + n) kt, (11)
где kt — изменение запасов капитала на одного работника; it — инвестиции на одного работника; dkt — амортизация на одного работника; nkt — прирост капитала, обусловленный приростом населения и занятостью в экономике.
Произведение nkt показывает потребность дополнительного капитала в расчете на одного работника, чтобы капиталовооруженность работника сохранилась на прежнем уровне.
Поскольку у = f(k), то условие устойчивого равновесия в экономике при неизменной капиталовооруженности:
k = sf(k) – (d + n) k (12)
Для того чтобы капиталовооруженность оставалась постоянной, капитал должен увеличиваться таким же темпом, что и население:
ΔY/Y = ΔL/L + ΔK/K = n. (13)
Включение в модель технического прогресса меняет исходную производственную функцию:
Y = F (К,L Е),
где Е — переменная, означающая эффективность труда.
Если предположить, что эффективность труда на одного работника растет с постоянным темпом g=0,03, то отдача от каждой единицы увеличивается на 3 %.
Поскольку рабочая сила растет темпом n, а отдача — темпом g, то общее число эффективных единиц труда — темпом n + g.
Оптимальная норма накопления по «золотому правилу», сформулированному Фелпсом, должна соответствовать условию:
МРК = d
т. е. предельный продукт капитала равен норме выбытия, а если учесть рост населения и технический прогресс
МРК = d + n + g
Оптимальная норма накопления (k *), соответствующая «золотому правилу», обеспечивает равновесный экономический рост с максимальным уровнем потребления.
