Выбор оптимального проекта может подразумевать отбор из заданной совокупности взаимно независимых проектов тех проектов, которые обеспечивают либо наибольший суммарный эффект, либо наименьшую величину затрат при некоторых ограничениях.
Если известна некоторая совокупность эффективных проектов, то каждый к-й проект будет характеризоваться положительной величиной интегрального эффекта (Эк) и потребностью в капитальных затратах (Зк). Введем вспомогательные (булевы) переменные хк, равные 1 для проектов, подлежащих реализации, и 0 для нереализуемых проектов. Булевыми называют переменные, которые принимают только значение 0 или 1. В этом случае задача сводится к нахождению такого сочетания булевых переменных {xij}, которые будут решением следующей оптимизационной задачи:
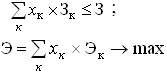
где З – суммарная величина всех капитальных затрат, достаточная для реализации хотя бы одного проекта;
Э – совокупный интегральный эффект от реализации отобранных проектов.
Если в качестве критерия выбора оптимального инвестиционного проекта использовать величину капитальных затрат, то оптимизационную задачу можно построить по-другому. Обозначим через сij i-й вид капитальных затрат, возникающих при реализации j-го проекта, а через хij – булеву переменную, равную 1 для проектов, подлежащих реализации, и 0 для нереализуемых проектов. Задача сводится к нахождению таких булевых переменных {xij}, которые будут решением следующей оптимизационной задачи:
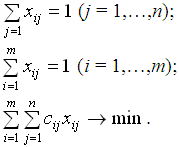
В обоих случаях построена оптимизационная задача целочисленного программирования, для которой имеются эффективные вычислительные методы, в том числе и для нахождения приближенного решения.
