Если известны вероятности реализации того или иного сценария, то вариационный метод можно дополнить вероятностной составляющей. Наличие различных сценариев будущего и соответствующих показателей эффективности позволяет говорить об этих показателях, как о случайных величинах, то есть величинах, которые могут принимать то или иное значение, и неизвестно заранее, какое именно.
Если известны вероятности осуществления сценариев реализации инвестиционного проекта и соответствующие показатели эффективности, то можно задать закон распределения показателей эффективности (как случайных величин). Законом распределения случайной величины называется соотношение между значениями случайной величины и соответствующими им вероятностями. На основании законов распределения рассчитываются обобщающие характеристики случайных величин, которые измеряют колебания их значений.
Таким образом, можно получить обобщающие характеристики, которые рассчитываются для случайных величин и которые измеряют колебания показателей эффективности. Чем эти колебания больше, тем выше рассеивание показателей эффективности вокруг среднего (или базового) значения и, следовательно, значительнее степень риска.
Стандартными характеристиками случайной величины и соответственно риска являются следующие показатели:
1) дисперсия – показатель, с помощью которого можно судить о рассеянии случайной величины относительно математического ожидания:
![]()
где Х – вектор значений случайной величины (в данном случае – значения показателей эффективности);
М(Х) – математическое ожидание случайной величины (показателя эффективности);
2) среднее квадратичное отклонение случайной величины рассчитывается по формуле
![]()
Кроме ожидаемых значений эффективности рассчитываются дополнительные показатели:
- риск неэффективности проекта (Рэ) – суммарная вероятность сценариев, при которых ЧДД становится отрицательным:
![]() где рj – вероятность реализации j-го сценария.
где рj – вероятность реализации j-го сценария.
Чем выше данный показатель, тем риск проекта больше;
- средний (ожидаемый) ущерб от реализации проекта в случае его неэффективности (Уэ) определяется по формуле
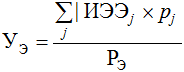
где |ИЭЭj| – чистый дисконтированный доход при реализации j-го сценария;
- премия за риск. ИЭЭ сценариев и ожидаемый эффект зависят от значения нормы дисконта, которая рассчитывается по формуле
i = d + h
Премия за риск (r) неполучения доходов, предусмотренных основным сценарием проекта, определяется из условия
ИЭЭОЖ(d+h) = ИЭЭОC(d+h+r)
где ИЭЭОЖ(d+h) – ожидаемый интегральный экономический эффект проекта, рассчитанный при безрисковой норме дисконта (d+h);
ИЭЭОC(d+h+r) – интегральный экономический эффект базового сценария, рассчитанный при норме дисконта (d+h+r), то есть включающей поправку на риск;
- ожидаемый ИЭЭ. В случае, когда какая-либо информация о вероятностях сценариев отсутствует (известно, что в сумме они составляют 1), расчет производится по формуле
ИЭЭОЖ = λ∙ИЭЭmax + (1-λ)∙ИЭЭmin
где ИЭЭmax и ИЭЭmin – наибольший и наименьший ИЭЭ при различных сценариях;
λ – специальный норматив для учета неопределенности ИЭЭ, отражающий систему предпочтений инвестора в условиях неопределенности.
