Прогнозирование составляет фундаментальную основу предпринимательской и управленческой деятельности в любой сфере деятельности при выполнении любой из базовых функций управления.
Многообразие проблем, возникающих при обеспечении жизнедеятельности предприятия и становящихся предметом прогнозирования и принятия управленческого решения, приводит к появлению большого количества разнонаправленных прогнозов, требующих определенной систематизации.
При выполнении прогнозирования в типовую последовательность операций включается:
- предпрогнозная ориентация на основе системно-структурного анализа объекта;
- постановка задачи для разработки прогноза – уточнение характеристик объекта, масштабов выпуска или рынка сбыта, установление периода прогнозирования, а также условий, ограничений и ожидаемого гипотетического результата;
- анализ и установление активных факторов прогнозного фона;
- формирование информационной базы по объекту прогноза и прогнозному фону (патенты, научно-техническая, экономическая информация и т. п.);
- разработка прогноза развития объекта и оценка его достоверности с учетом действия факторов прогнозного фона;
- анализ результатов прогнозирования;
- выработка рекомендаций по результатам анализа для принятия решений в сфере управления.
Специфика проблемы или задачи прогнозирования могут потребовать изменения и дополнения перечисленных операций.
В процессе прогнозирования используют два подхода:
- индуктивный подход – рассмотрение проблем от частного к общему, т. е. на основании фактических или зарегистрированных данных (эксперимента или развития процесса) об объекте устанавливается тенденция (или закономерность) общего развития объекта, которая и используется при обосновании прогноза;
- дедуктивный подход – определение общих тенденций или закономерностей развития анализируемой области техники, а затем – на основе выявленной общей перспективы – уровней и путей развития отдельных направлений, а также конкретных технических характеристик интересующих в данном случае объектов прогнозирования.
Индуктивному подходу в наибольшей степени соответствуют методы поискового прогнозирования, а дедуктивному – нормативного.
При поисковом прогнозировании состояние объекта в будущем определяется закономерностями, выявленными по частным результатам опыта (эксперимента) его поведения в прошлом и настоящем. В этом случае прогнозирование осуществляется от имеющегося уровня знаний, а конечные результаты развития объекта составляют содержание прогноза.
В свою очередь, нормативное прогнозирование ориентировано на то, что задается конечная цель (или закономерность) развития (поведения) объекта в будущем, а содержанием прогноза становится определение частных путей, средств и сроков достижения цели. Прогнозирование в этом случае осуществляется от заданной цели как бы навстречу ходу времени.
Современная прогностика располагает большим арсеналом методов прогнозирования, но ни один из них не может быть признан универсальным.
На выбор метода прогнозирования влияют следующие факторы:
- существо практической проблемы, подлежащей решению;
- динамические характеристики объекта прогнозирования и рыночной среды;
- вид и характер имеющейся информации, типовое представление объекта прогнозирования;
- фаза жизненного цикла товара, услуги или организационно-производственной системы;
- период упреждения и его соотношение с предполагаемой длительностью жизненного цикла товара, услуги, организационно-производственной системы;
- требования к результатам прогнозирования и т. п.
Рассмотрим некоторые методы прогнозирования более подробно.
Метод программного прогнозирования, предложенный академиком В. М. Глушковым, – обобщение, с одной стороны, известного метода «Дельфи», а с другой – не менее известного метода PERT (метод сетевого планирования управления).
Метод программного прогнозирования служит для определения вероятности наступления тех или иных событий и оценки вероятного времени их наступления. Перед началом работы следует иметь классификатор типов событий, которые предстоит анализировать, и начальный список экспертов по проблемам. Для каждого типа проблем указывается априорный вес каждого эксперта, например, по стабильной системе. Первоначально эти веса определяются самими экспертами, в последующем они могут уточняться с помощью объективных методов.
Первый шаг применения этого метода состоит в постановке задачи, т. е. перечислении событий, время и вероятность которых называют заключительными. В задачу эксперта входит, прежде всего, определение условий, при наличии которых возможна оценка им того или иного события.
Предположим, например, что событие S, которое предстоит оценить, есть создание новой автоматической линии. Эксперт должен представить себя в положении конструктора, которому реально поручено выполнять эту задачу. Тогда в качестве условий он может, например, выставить выполнение двух событий S1 и S2. Первое представляет собой наличие необходимого специального оборудования, второе – наличие соответствующих технологических процессов.
Для повышения ответственности экспертов можно принять, что факт выставления ими тех или иных условий при оценке события есть одновременно и обязательство (в случае выполнения этих условий в будущем) взяться за реальное осуществление оцениваемого события. Подобное соглашение способствовало бы одновременно повышению объективности оценки экспертами своих собственных весовых коэффициентов.
В общем виде условие F может представлять собой произвольную логическую функцию f (S1, S2, S3 …, Sk) от некоторых независимых (с точки зрения эксперта) событий S1, S2, S3 …, Sk. Эта функция строится с помощью конечного числа дизъюнкций, конъюнкций и отрицаний.
Далее эксперт должен оценить условную вероятность PF(S) наступления события S при выполнении условия F и наиболее вероятную величину времени TF(S) между временем выполнения условия F и временем наступления события S (если оно вообще наступит). При этом, разумеется, не исключается (и даже желательна) возможность оценки безусловной вероятности наступления события S и полного времени, считая от настоящего момента, до момента его наступления. Этот случай соответствует обращению условия F в тождественно истинное событие (полному множеству событий S1, S2 , S3 …, Sk).
Анкеты экспертов служат прежде всего для построения сети событий, аналогичной пертовской сети. При этом каждой оценке эксперта [PF (S) и TF (S)] соответствует работа на пертовской сети, TF (S) представляет собой оценку продолжительности этой работы. События событий S1, S2, S3 …, Sk , входящие в условие F = f (S1, S2 , S3 …, Sk), соединяются с событием S фиктивными работами нулевой продолжительности.
Для упрощения предположим, что получающаяся сеть удовлетворяет обычным пертовским требованиям, в частности требованию отсутствия петель. С этой целью при обработке анкет экспертом принимаются специальные меры (возвращение анкет для исключения тех или иных условий, аннулирование частей анкеты и т. д.). Впрочем, в отличие от классического метода PERT предлагаемая методика может быть расширена таким образом, чтобы включить в рассмотрение также и сети с петлями.
Ввиду того, что ответы экспертов вводят, вообще говоря, новые события, последние посылаются для оценки другим экспертам. В этом участвуют и эксперты, принявшие участие в предыдущем туре: им посылается фрагмент сети, полученной на предыдущем туре. Этот фрагмент (L – окрестность события S) включает перечень всех элементарных событий S1, S2 , S3 ….Sn, выставленных в числе условий хотя бы одним экспертом, принимавшим участие в оценке данного события S. Эксперты по данному событию S в новом туре могут менять свои условия, включая в них любые элементарные S1, S2 , S3 ….Sn (и меняя, соответственно, свои оценки).
Полезно также, чтобы эксперт, выставивший в качестве условий те или иные события S1, S2, S3 …, Sn, указывал в анкете имена возможных экспертов для оценки этих событий. Тем самым список экспертов будет расширяться до тех пор, пока не произойдет стабилизация сети.
В стабилизационной сети без петель все события разбиваются на слои. В первый слой входят все события, получившие только безусловные оценки вероятности (и ожидаемого времени) своего наступления. А для оценки событий, лежащих в i-ом слое (I > 2), в качестве условий используются лишь события из слоев с номерами, меньшими, чем I. Дальнейшая обработка построенной сети производится следующим образом. Последовательно, слой за слоем, вычисляются абсолютные вероятности наступления всех составляющих слой событий и распределение абсолютного времени ожидаемого их наступления, а также оценки разброса этих величин (среднеквадратичные ошибки).
Распределение абсолютного времени с практической точки зрения наиболее удобно задавать, фиксируя заранее конечное число моментов времени [например, t1 = 2 006, t2 = 2 008, t3 = 2 010, t4 = 2 012, всегда добавляя к ним бесконечное время; в данном случае t5 = ∞ (бесконечность)].
Распределение абсолютного времени наступления любого события рассматриваемой сети будет характеризоваться вектором вероятностей (P1, P2, …Pk … P∞), где Pi(S) и представляет собой оценку вероятности наступления события S до момента времени ti. В частности, P∞ = P представляет собой оценку безусловной вероятности наступления события в неограниченный период времени. Для компонент вектора среднеквадратичных погрешностей вводятся соответствующие обозначения соответствующих оценок.
Оценка вероятности Pi производится на основе обычного усреднения (с учетом весов экспертов) оценок, даваемых отдельными экспертами. Их получают последовательно, слой за слоем.
Для события S из первого слоя экспертом дается оценка абсолютной вероятности P и абсолютного времени t наступления этого события. Тогда соответствующие (одиночные) оценки данного эксперта дадут значения Pi = 0 для всех ti < t и Pi = Р для всех ti ≥ t.
Если же событие S не из первого слоя и для него дана оценка условной вероятности q и относительного времени выполнения данного события S при условии F=f (S1 , S2 ,…, Sk), то для события S1 , S2 ,…, Sk по принятому нами соглашению должны уже быть известны абсолютные (усредненные) оценки вероятностей их наступления и соответствующие оценки для всех других компонентов вектора вероятностей.
Для любой из этих компонент Pi (включая и P∞) будут иметь место известные соотношения:
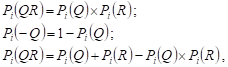
где Q и R – любая пара независимых событий.
Эти соотношения в силу нашего предположения о независимости событий S1, S2,…, Sk дают возможность подсчитать значение соответствующей компоненты Pi (F) вектора вероятностей для события F.
Повторяя этот процесс и проводя необходимые усреднения, мы получим, в конце концов, оценку вектора вероятностей и разброса его значений для интересующего нас заключительного события. При дальнейшей работе с сетью опросы экспертов можно систематически повторять. Изучая динамику изменения оценок вместе с информацией о действительном времени наступления тех или иных событий, можно предложить различные приемы внесения поправок в вес оценок экспертов.
Выбор того или иного из этих приемов зависит от степени правильности начальных оценок по сравнению с более поздними, от желания учитывать степень правильности не только конечного результата (оценки времени), но и путей его достижения (правильности выбора условий).
Работа с построенной сетью может предусматривать возможность уточнения тех или иных частных оценок для составляющих ее событий (например, путем привлечения новых экспертов или постановкой новых исследований). Для каждого события это уточнение будет требовать определенных затрат (вообще говоря, тем больших, чем выше слой, которому принадлежит данное событие). Необходимо поэтому разработать методику рационального выбора этих уточнений.
Предположим, что из каких-либо соображений, находящихся вне сферы наших рассмотрений, установлено, что наибольший интерес представляет уточнение оценки вероятности Pi (S) наступления заключительного события S до момента времени ti.
Для каждого события Si, входящего в построенную сеть, определим изменение оценки вероятности Pi (S) при максимальных изменениях компонент вектора вероятностей для события S, допускаемых экспертами.
Стоимость эксперимента по уточнению оценки вектора вероятностей для события S, отнесенную к величине указанного изменения, естественно выбрать в качестве критерия для выбора Si, оценка вектора вероятностей которого подлежит уточнению в первую очередь.
Метод эвристического прогнозирования
Основная задача, стоящая перед специалистами по анализу и проектированию больших систем, в общем случае заключается в нахождении оптимальных способов создания более эффективных систем – либо вновь проектируемых, либо модернизируемых. Сложность решения этой задачи состоит, прежде всего, в том, что здесь обычно нет возможности найти решение чисто математическими методами, поскольку, как правило, не удается точно определить величины (функционалы), подлежащие оптимизации (экстремализации) в математическом смысле. Это связано не только со сложностью описания функционирования больших систем, но и со спецификой целей, для достижения которых предназначена система.
Методом эвристического прогнозирования называется метод получения и специализированной обработки прогнозных оценок объекта путем систематизированного опроса высококвалифицированных специалистов (экспертов) в узкой области науки, техники или производства. Прогнозные экспертные оценки отражают индивидуальное суждение специалиста относительно перспектив развития его области и основаны на мобилизации профессионального опыта и интуиции.
Элементы этого метода – сбор и обработка суждений экспертов, высказанных на основе профессионального опыта и интуиции. Однако он отличается от описанных выше методов большей четкостью теоретических основ, способами формирования анкет и таблиц, порядком работы с экспертами и алгоритмом обработки полученной информации. Эвристическим данный метод назван в связи с однородностью форм мыслительной деятельности эксперта при решении научной проблемы и при оценке перспектив развития объекта прогнозирования, а также в связи с использованием экспертами специфических приемов, приводящих к правдоподобным умозаключениям.
