Методы моделирования в исследовании

Исследование неизбежно связано с абстракцией и формализацией изучаемой действительности, представлением ее в виде модели системы, процесса, среды. В исследовании модель (от лат. modelium – мера, образ, способ) рассматривается как наиболее эффективное средство познания реальности.

Модель – это образ реального объекта (процесса) в материальной или идеальной форме (описанный знаковыми средствами или на каком-либо языке), отражающий существенные свойства моделируемого объекта (процесса) и замещающий его в ходе исследования и управления.

Главной характеристикой модели можно считать упрощение реальной жизненной ситуации, к которой она относится. Поскольку форма модели менее сложна, а не относящиеся к делу данные, затуманивающие проблему в реальной жизни, устраняются, модель зачастую повышает способность руководителя к пониманию и разрешению встающих перед ним проблем.

В настоящее время существует множество используемых современными организациями моделей, а также задач, для решения которых они наиболее пригодны. Можно выделить три базовых типа моделей. Речь идет о физических, аналоговых и математических моделях.

Физическая модель представляет то, что исследуется с помощью увеличенного или уменьшенного описания объекта или системы.

Примеры физических моделей – синька чертежа завода, его уменьшенная фактическая модель, уменьшенный в определенном масштабе чертеж проектировщика. Такая физическая модель упрощает визуальное восприятие и помогает установить, сможет ли конкретное оборудование физически разместиться в пределах отведенного для него места, а также разрешить сопряженные проблемы, например размещение дверей, ускоряющее движение людей и материалов.

Автомобильные и авиационные предприятия всегда изготавливают физически уменьшенные копии новых средств передвижения, чтобы проверить определенные характеристики, например аэродинамическое сопротивление. Будучи точной копией, модель должна вести себя аналогично разрабатываемому новому автомобилю или самолету, но при этом ее стоимость много меньше настоящего. Подобным образом строительные компании всегда строят миниатюрную модель, прежде чем начать строительство производственного или административного корпуса или склада.

Аналоговая модель представляет исследуемый объект аналогом, который ведет себя как реальный объект, но не выглядит как таковой. График, иллюстрирующий соотношение между объемом производства и издержками, – это аналоговая модель. График показывает, как уровень производства влияет на издержки.

Другой пример аналоговой модели – организационная схема. Выстраивая ее, руководство в состоянии легко представить себе цепи прохождения команд и формальную зависимость между индивидами и деятельностью. Такая аналоговая модель – явно более простой и эффективный способ восприятия и определения сложных взаимосвязей структуры крупной организации, чем, скажем, составление перечня взаимосвязей всех работников.

В математической модели, называемой также символической, используются символы для описания свойств или характеристик объекта или события. Пример математической модели и ее аналитической силы как средства, помогающего нам понимать исключительно сложные проблемы, – известная формула А. Эйнштейна Е = mc². Если бы А. Эйнштейн не смог построить эту математическую модель, в которой символы заменяют реальность, маловероятно, чтобы у физиков появилась даже отдаленная идея о взаимосвязи материи и энергии.

Экономико-математическое моделирование

Данная разновидность моделирования обладает рядом существенных особенностей, связанных как с объектом моделирования, так и с применяемыми аппаратом и средствами моделирования, поэтому целесообразно более детально проанализировать последовательность и содержание его этапов.

Постановка экономической проблемы и ее качественный анализ. На этом этапе требуется сформулировать сущность проблемы, принимаемые предпосылки и допущения. Необходимо выделить важнейшие черты и свойства моделируемого объекта, изучить структуру и взаимосвязь его элементов, хотя бы предварительно сформулировать гипотезы, объясняющие поведение и развитие объекта.

Построение математической модели. Это этап формализации экономической проблемы, т. е. выражения ее в виде конкретных математических зависимостей. Процесс построения модели проходит в свою очередь несколько стадий. Сначала определяется тип экономико-математической модели, изучаются возможности ее применения в данной задаче, уточняется конкретный перечень переменных и параметров и форма связей. Для некоторых сложных объектов целесообразно строить несколько разноаспектных моделей. При этом каждая модель выделяет лишь некоторые стороны объекта, а другие стороны учитываются агрегировано и приближенно.

Оправдано стремление построить модель, относящуюся к хорошо изученному классу математических задач, что может потребовать некоторого упрощения исходных предпосылок модели, не искажающего основные черты моделируемого объекта. Однако возможна и такая ситуация, когда формализация проблемы приводит к неизвестной ранее математической структуре.

Математический анализ модели. На этом этапе чисто математическими приемами исследования выявляются общие свойства модели и ее решения. В частности, важный момент – доказательство существования решения сформулированной задачи. При аналитическом исследовании выясняется, единственно ли решение, какие переменные могут входить в решение, в каких пределах они изменяются, каковы тенденции их изменения и т. д. Однако модели сложных экономических объектов с большим трудом поддаются аналитическому исследованию. В таких случаях переходят к численным методам исследования.

Подготовка исходной информации. В экономических задачах это, как правило, наиболее трудоемкий этап моделирования, так как дело не сводится к пассивному сбору данных. Математическое моделирование предъявляет жесткие требования к системе информации. Кроме того, надо принимать во внимание не только принципиальную возможность подготовки информации требуемого качества, но и затраты на подготовку информационных массивов.

В процессе подготовки информации используются методы теории вероятности, теоретической и математической статистики для организации выборочных обследований, оценки достоверности данных и т. д. При системном экономико-математическом моделировании результаты функционирования одних моделей служат исходной информацией для других.

Численное решение. Этот этап включает разработку алгоритмов численного решения задачи, подготовку программ на ЭВМ и непосредственное проведение расчетов; при этом значительную трудность составляет большая размерность экономических задач. Обычно расчеты на основе экономико-математической модели носят многовариантный характер. Многочисленные модельные эксперименты, изучение поведения модели при различных условиях возможно проводить благодаря быстродействию современных ЭВМ. Численное решение существенно дополняет результаты аналитического исследования, а для многих моделей оно единственное возможное.

Анализ численных результатов и их применение. На этом этапе, прежде всего, решается важнейший вопрос о правильности и полноте результатов моделирования и применимости их как в практической деятельности, так и в целях усовершенствования модели, поэтому в первую очередь должна быть проведена проверка адекватности модели по тем свойствам, которые выбраны в качестве существенных. Другими словами, должны быть произведены верификация (проверка правильности структуры модели) и ее валидация (проверка соответствия данных, полученных на основе модели, реальному процессу).

Перечисленные этапы экономико-математического моделирования находятся в тесной взаимосвязи, в частности могут иметь место возвратные связи этапов. Так, на этапе построения модели может выясниться, что постановка задачи или противоречива, или приводит к слишком сложной математической модели. В этом случае исходная постановка задачи должна быть скорректирована.

Наиболее часто необходимость возврата к предшествующим этапам моделирования возникает на этапе подготовки исходной информации. Если необходимая информация отсутствует или затраты на ее подготовку слишком велики, приходится возвращаться к этапам постановки задачи и ее формализации, чтобы приспособиться к доступной исследователю информации.

Процесс моделирования, как правило, носит циклический характер. Недостатки, которые не удается исправить на тех или иных этапах моделирования, устраняются в последующих циклах. Однако результаты каждого цикла имеют и вполне самостоятельные значения. Можно начать исследование с построения простой модели и, получив полезные результаты, перейти затем к созданию более сложной и более совершенной модели, включающей в себя новые условия и более точные математические значения.

Классификация экономико-математических моделей

Первая классификация экономико-математических моделей была приведена в монографии Т. Нейлора «Машинные имитационные эксперименты с моделями экономических систем» в 1971 г.

Однако в настоящее время единой системы классификации не существует. Обычно выделяют более десяти основных признаков классификации. Рассмотрим выделенные классификационные признаки подробнее.

По общему целевому назначению экономико-математические модели делятся на теоретико-аналитические, используемые при изучении общих свойств и закономерностей экономических процессов, и прикладные, применяемые в решении конкретных экономических задач анализа, прогнозирования и управления.

По степени агрегирования объектов моделирования модели делятся на макро- и микроэкономические, хотя между ними и нет четкого разграничения. К первым из них относят модели, отражающие функционирование экономики как единого целого, в то время как микроэкономические модели связаны, как правило, с такими звеньями экономики, как предприятие и фирма.

По конкретному предназначению, т. е. по цели создания и применения, выделяют:

• балансовые модели, выражающие требование соответствия наличия ресурсов и их использования;
• трендовые модели, в которых развитие моделируемой экономической системы отражается через тренд (длительную тенденцию) ее основных показателей;
• оптимизационные модели, предназначенные для выбора наилучшего варианта из определенного числа вариантов производства, распределения или потребления;
• имитационные модели, предназначенные для использования в процессе машинной имитации изучаемых систем или процессов, и др.

По типу информации, используемой в модели, экономико-математические модели делятся на аналитические, построенные на априорной информации, и идентифицируемые, построенные на апостериорной информации.

По учету фактора времени модели подразделяются на статические, в которых все зависимости отнесены к одному моменту времени, и динамические, описывающие экономические системы в развитии.

По учету фактора неопределенности модели делятся на детерминированные, если в них результаты на «выходе» однозначно определяются управляющими воздействиями, и стохастические (вероятностные), если при задании на «входе» модели определенной совокупности значений на ее «выходе» могут получаться различные результаты в зависимости от действия случайного фактора.

По типу математического аппарата, используемого в модели, т. е. по характеристике математических объектов, включенных в модель, могут быть выделены матричные модели, модели линейного и нелинейного программирования, корреляционно-регрессионные модели, модели теории массового обслуживания, модели сетевого планирования и управления, модели теории игр и т. д.

По типу подхода к изучаемым социально-экономическим системам выделяют дескриптивные и нормативные модели. При дескриптивном (описательном) подходе получают модели, предназначенные для описания и объяснения фактически наблюдаемых явлений или для прогноза этих явлений. В качестве примера дескриптивных моделей можно привести названные ранее балансовые и трендовые модели. При нормативном подходе интересуются не тем, каким образом устроена и развивается экономическая система, а тем, как она должна быть устроена и как должна действовать согласно определенным критериям.

Модели теории игр

Одна из важнейших переменных, от которой зависит успех организации, – конкурентоспособность. Очевидно, что способность прогнозировать действия конкурентов означает преимущество для любой организации. Теория игр – это метод моделирования воздействия принятого решения на конкурентов.

Теорию игр изначально разрабатывали военные с тем, чтобы в стратегии можно было учесть возможные действия противника. В бизнесе игровые модели используются для прогнозирования реакции конкурентов на изменение цен, новые компании поддержки сбыта, предложения дополнительного обслуживания, модификацию и освоение новой продукции. Если, например, с помощью теории игр руководство устанавливает, что при повышении цен конкуренты не сделают того же, оно, вероятно, должно отказаться от этого шага, чтобы не попасть в невыгодное положение в конкурентной борьбе.

Теория игр используется не так часто, как другие описываемые модели, так как ситуация реального мира зачастую очень сложна и настолько быстро изменяется, что невозможно точно спрогнозировать, как отреагируют конкуренты на изменение тактики фирмы. Тем не менее, теория игр полезна, когда необходимо определить наиболее важные и требующие учета факторы в ситуации принятия решения в условиях конкурентной борьбы. Эта информация важна, поскольку позволяет руководству учесть дополнительные переменные или факторы, могущие повлиять на ситуацию.

Модели теории массового обслуживания

Модели теории массового обслуживания используются для определения оптимального числа каналов обслуживания по отношению к потребности в них. К ситуациям, в которых модели теории массового обслуживания могут быть полезны, можно отнести ожидание клиентами банка свободного кассира, очередь грузовиков под разгрузку на склад. Если, например, клиентам приходится слишком долго ждать кассира, они могут решить перенести свои счета в другой банк. Подобным образом, если грузовикам приходится слишком долго дожидаться разгрузки, они не смогут выполнить положенное количество поездок за день.

Таким образом, принципиальная проблема заключается в уравновешивании расходов на дополнительные каналы обслуживания: требуется больше людей для разгрузки грузовиков, больше кассиров и потерь от обслуживания на уровне ниже оптимального.

Так, модели очередей снабжают руководство инструментом определения оптимального числа каналов обслуживания, которые необходимо иметь, чтобы в случаях чрезмерно малого и чрезмерно большого их количества сбалансировать издержки.

В настоящее время теоретически наиболее разработаны и удобны в практических приложениях методы решения таких задач массового обслуживания, в которых входящий поток требований простейший (пуассоновский).

Для простейшего потока частота поступления требований в систему подчиняется закону Пуассона, т. е. вероятность поступления P_k (t) за время t равно k:

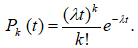
Важная характеристика систем массового обслуживания – время обслуживания требований в системе. Время обслуживания одного требования – это, как правило, случайная величина и, следовательно, может быть описано законом распределения. Наибольшее распространение в теории, особенно в практических приложениях, получил экспоненциальный закон распределения времени обслуживания. Функция распределения для этого закона имеет вид:

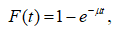
т. е. вероятность того, что время обслуживания не превосходит некоторой величины t, определяется этой формулой, где μ – параметр экспоненциального закона распределения времени, необходимого для обслуживания требований в системе, т. е. величина, обратная среднему времени обслуживания t_об:

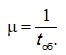
Рассмотрим аналитические модели наиболее распространенных систем массового обслуживания с ожиданием, т. е. таких систем, в которых требования, поступившие в момент, когда все обслуживающие каналы заняты, ставятся в очередь и обслуживаются по мере освобождения каналов.

Общая постановка задачи состоит в следующем. Система имеет n обслуживающих каналов, каждый из которых может одновременно обслуживать только одно требование. В систему поступает простейший (пуассоновский) поток требований с параметром λ.

Если в момент поступления очередного требования в системе на обслуживании уже находится не меньше n требований (т. е. все каналы заняты), то это требование становится в очередь и ждет начала обслуживания.

Время обслуживания каждого требования t_об – случайная величина, которая подчиняется экспоненциальному закону распределения с параметром μ.

Системы массового обслуживания с ожиданием можно разбить на две большие группы: замкнутые и разомкнутые. К замкнутым относятся системы, в которых поступающий поток требований возникает в самой системе и ограничен. Например, мастер, задача которого – наладка станков в цехе, должен периодически их обслуживать. Каждый налаженный станок становится потенциальным источником требований на наладку. В подобных системах общее число циркулирующих требований, конечно, чаще всего постоянно. Если питающий источник обладает бесконечным числом требований, то системы называются разомкнутыми. Примерами подобных систем могут служить магазины, кассы вокзалов, портов и т. п. Для этих систем поступающий поток требований можно считать неограниченным.

Отмеченные особенности функционирования систем этих двух видов накладывают определенные условия на используемый математический аппарат. Расчет характеристик работы систем массового обслуживания различного вида может быть проведен на основе расчета вероятностей состояний систем (так называемые формулы Эрланга).

Рассмотрим алгоритмы, предназначенные для расчета качества функционирования разомкнутой системы массового обслуживания с ожиданием.

При изучении таких систем рассчитывают различные показатели эффективности обслуживающей системы. В качестве основных показателей могут быть: вероятность того, что все каналы свободны или заняты; математическое ожидание длины очереди (средняя длина очереди); коэффициенты занятости и простоя каналов обслуживания и др.

Введем в рассмотрение параметр 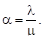Заметим, что если 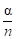<1, то очередь не может расти безгранично. Это условие имеет следующий смысл: λ – среднее число требований, поступающих за единицу времени; 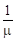– среднее время обслуживания одним каналом одного требования, тогда 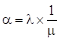– среднее число каналов, которое необходимо иметь, чтобы обслуживать в единицу времени все поступающие требования. Поэтому условие 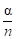<1 означает, что число обслуживающих каналов должно быть больше среднего числа каналов, необходимых для того, чтобы за единицу времени обслужить все поступившие требования.

Важнейшие характеристики работы систем массового обслуживания:

1) вероятность того, что все обслуживающие каналы свободны:

;

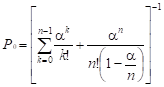2) вероятность того, что занято ровно k обслуживающих каналов при условии, что общее число требований, находящихся на обслуживании, не превосходит числа обслуживающих параметров:

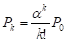, при 1 ≤ k ≤ n;

3) вероятность того, что в системе находится k требований в случае, когда их число больше числа обслуживающих каналов:

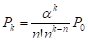, при k ≥ n;

4) вероятность того, что все обслуживающие каналы заняты:

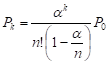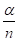, при <1;

5) среднее время ожидания требования в системе:

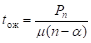, при n < 1;

6) средняя длина очереди:

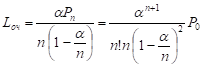, при n < 1;

7) коэффициент простоя каналов:

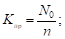
8) среднее число занятых обслуживанием каналов:

;

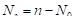9) коэффициент загрузки каналов:

.

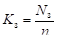При рассмотрении замкнутых систем массового обслуживания к постановке задачи следует добавить условие: поток поступающих требований ограничен, т. е. в системе одновременно не может находиться больше m требований (m – число обслуживаемых объектов).

Имитационное моделирование

Все описанные выше модели подразумевают применение имитации в широком смысле, поскольку все они – заменители реальности. Тем не менее, как метод моделирования имитация конкретно обозначает процесс создания модели и ее экспериментальное применение для определения изменений реальной ситуации. Аэродинамическая труба – пример физически осязаемой имитационной модели, используемой для проверки характеристик разрабатываемых самолетов и автомобилей. Специалисты по производству и финансам могут разработать модели, позволяющие имитировать ожидаемый прирост производительности и прибылей в результате применения новой технологии или изменений состава рабочей силы. Специалист по маркетингу может создать модель для имитации ожидаемого объема сбыта в связи с изменением цен или рекламы продукции.

Имитация используется в ситуациях, слишком сложных для математических методов типа линейного программирования. Это может быть связано с чрезмерно большим числом переменных, трудностью математического анализа определенных зависимостей между переменными или высоким уровнем неопределенности.

Итак, имитация – это часто весьма практичный способ подстановки модели на место реальной системы или натурного прототипа. Экспериментируя на модели системы, можно установить, как она будет реагировать на определенные изменения или события в случае, если отсутствует возможность наблюдать эту систему в реальности. Если результаты экспериментирования с использованием имитационной модели свидетельствуют о том, что модификация ведет к улучшению, руководитель может с большей уверенностью принимать решение об осуществлении изменений в реальной системе.