Метод Монте-Карло представляет собой расчетный численный способ решения исследовательских задач математического характера на основе моделирования случайных величин и формализованного описания неопределенности. Этот способ называется также методом статистических испытаний, так как на основе статистических данных и различного рода ограничений позволяет сформировать имитационные модели и создать множество сценариев реализации задач исследования и выбрать наиболее вероятный из них.
Разработчиками данного метода принято считать американских математиков Дж. Неймана и С. Улама (конец 40-х годов ХХ в.). В нашей стране он стал известен в 1955–1956 гг. Основа метода была известна в период, когда статистики начали решать задачи с помощью случайных выборок. Однако широкого распространения данный метод не мог получить из-за трудоемких работ моделирования случайных величин. Только с появлением ЭВМ стало возможным широкое распространение такого универсального численного метода.
Имитационное моделирование по методу Монте-Карло позволяет построить математическую модель для проекта с неопределенными значениями параметров и, зная вероятностные распределения параметров проекта, а также связь между изменениями параметров (корреляцию), получить распределение доходности проекта.
Блок-схема, представленная на рисунке, отражает укрупненную схему работы с моделью.
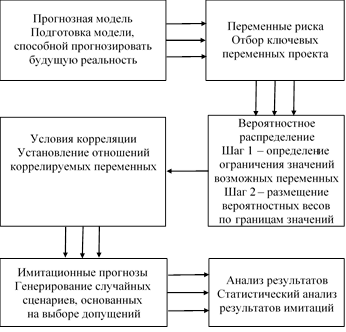
Блок-схема реализации метода Монте-Карло
Применение метода имитации Монте-Карло требует использования специальных математических пакетов (например, специализированного программного пакета Гарвардского университета под названием Risk-Master), позволяющих в диалоговом режиме осуществить процедуру подготовки информации к анализу рисков инвестиционного проекта по методу Монте-Карло и провести сами расчеты.
Первый шаг при применении метода имитации состоит в определении функции распределения каждой переменной, которая оказывает влияние на формирование потока наличности. Как правило, предполагается, что функция распределения являются нормальной, и, следовательно, для того чтобы задать ее, необходимо определить только два момента (математическое ожидание и дисперсию). Как только функция распределения определена, можно применять процедуру Монте-Карло.
Рассмотрим алгоритм метода имитации Монте-Карло.
Шаг 1. Опираясь на использование статистического пакета, случайным образом выбираем, основываясь на вероятностной функции распределения, значение переменной, которая является одним из параметров определения потока наличности.
Шаг 2. Выбранное значение случайной величины наряду со значениями переменных, которые являются экзогенными переменными, используется при подсчете чистой приведенной стоимости проекта.
Шаги 1 и 2 повторяются большое количество раз, например 1 000, и полученные 1 000 значений чистой приведенной стоимости проекта используются для построения плотности распределения величины чистой приведенной стоимости со своим собственным математическим ожиданием и стандартным отклонением.
Используя значения математического ожидания и стандартного отклонения, можно вычислить коэффициент вариации чистой приведенной стоимости проекта и затем оценить индивидуальный риск проекта.
Теперь необходимо определить минимальное и максимальное значения критической переменной, а для переменной с пошаговым распределением помимо этих двух – еще и остальные значения, принимаемые ею. Границы варьирования переменной определяют, просто исходя из всего спектра возможных значений.
По прошлым наблюдениям за переменной можно установить частоту, с которой та принимает соответствующие значения. В этом случае вероятностное распределение есть то же самое частотное распределение, показывающее частоту встречаемости значения, правда, в относительном масштабе (от 0 до 1). Вероятностное распределение регулирует вероятность выбора значений из определенного интервала. В соответствии с заданным распределением модель оценки рисков будет выбирать произвольные значения переменной. До рассмотрения рисков подразумевалось, что переменная принимает одно определенное нами значение с вероятностью 1. И через единственную итерацию расчетов мы получали однозначно определенный результат. В рамках модели вероятностного анализа рисков проводится большое число итераций, позволяющих установить, как ведет себя результативный показатель (в каких пределах колеблется, как распределен) при подстановке в модель различных значений переменной в соответствии с заданным распределением.
Задача аналитика, занимающегося анализом риска, состоит в том, чтобы хотя бы приблизительно определить для исследуемой переменной (фактора) вид вероятностного распределения. При этом основные вероятностные распределения, используемые в анализе рисков, могут быть следующими: нормальное, постоянное, треугольное, пошаговое. Эксперт присваивает переменной вероятностное распределение, исходя из своих количественных ожиданий, и делает выбор из двух категорий распределений: симметричных (например, нормальное, постоянное, треугольное) и несимметричных (например пошаговое распределение).
Существование коррелированных переменных в проектном анализе вызывает порой проблему. Так, без учета коррелированности, скажем, двух переменных компьютер, посчитав их полностью независимыми, генерирует нереалистичные проектные сценарии. Допустим цена и количество проданного продукта есть две отрицательно коррелированные переменные. Если не будет уточнена связь между переменными (коэффициент корреляции), то возможны сценарии, случайно вырабатываемые компьютером, где цена и количество проданной продукции будут вместе либо высоки, либо низки, что, естественно, негативно отразится на результате.
Проведение расчетных итераций является полностью компьютеризированной частью анализа рисков проекта: 200–500 итераций обычно достаточно для хорошей репрезентативной выборки. В процессе каждой итерации происходит случайный выбор значений ключевых переменных из специфицированного интервала в соответствии с вероятностными распределениями и условиями корреляции. Затем рассчитываются и сохраняются результативные показатели (например NPV). И так далее, от итерации к итерации.
Завершающая стадия анализа проектных рисков – интерпретация результатов, собранных в процессе итерационных расчетов. Результаты анализа рисков можно представить в виде профиля риска. На нем графически показывается вероятность каждого возможного случая (имеются в виду вероятности возможных значений результативного показателя).
Часто при сравнении вариантов капиталовложений удобнее пользоваться кривой, построенной на основе суммы вероятностей (кумулятивный профиль риска). Такая кривая показывает вероятности того, что результативный показатель проекта будет больше или меньше определенного значения. Проектный риск, таким образом, описывается положением и наклоном кумулятивного профиля риска.
Кумулятивный (интегральный, накопленный) профиль риска показывает кумулятивное вероятностное распределение чистой текущей стоимости (NPV), с точки зрения банкира, предпринимателя и экономиста, на определенный проект. Вероятность того, что NPV < 0, с точки зрения экономиста, – около 0,4, в то время как для предпринимателя эта вероятность менее 0,2. С точки зрения банкира, проект кажется совсем безопасным, так как вероятность того, что NPV > 0, около 95%.
Будем исходить из того, что проект подлежит рассмотрению и считается выгодным, в случае, если NPV > 0. При сравнении нескольких одноцелевых проектов выбирается тот, у которого NPV больше при соблюдении сказанного в предыдущем предложении.
Рассмотрим пять случаев принятия решений. Случаи 1–3 имеют дело с решением инвестировать в отдельно взятый проект, тогда как случаи 4, 5 относятся к решению-выбору из альтернативных проектов. В каждом случае рассматривается как кумулятивный, так и некумулятивный профили риска для сравнительных целей. Кумулятивный профиль риска более полезен в случае выбора наилучшего проекта из представленных альтернатив, в то время как некумулятивный профиль риска лучше индуцирует вид распределения и показателен для понимания концепций, связанных с определением математического ожидания. Анализ базируется на показателе чистой текущей стоимости.
Случай 1. Минимальное возможное значение NPV выше, чем нулевое (кривая 1).
Вероятность отрицательного NPV равна 0, так как нижний конец кумулятивного профиля риска лежит справа от нулевого значения NPV. Так как данный проект имеет положительное значение NPV во всех случаях, ясно, что проект принимается.
Случай 2. Максимальное возможное значение NPV ниже нулевого (кривая 2).
Вероятность положительного NPV равна 0, так как верхний конец кумулятивного профиля риска лежит слева от нулевого значения NPV. Поскольку данный проект имеет отрицательное значение NPV во всех случаях, ясно, что проект не принимается.
Случай 3. Максимальное значение NPV больше, а минимальное меньше нулевого (кривая 3).
Вероятность нулевого NPV больше, чем 0, но меньше, чем 1, так как вертикаль нулевого NPV пересекает кумулятивный профиль рисков. Так как NPV может быть как отрицательным, так и положительным, решение будет зависеть от предрасположенности к риску инвестора. По-видимому, если математическое ожидание NPV меньше или равно 0 (пик профиля рисков слева от вертикали или вертикаль точно проходит по пику), проект должен отклоняться от дальнейшего рассмотрения.
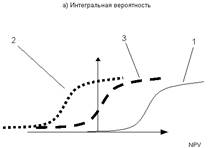
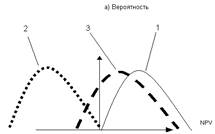
График распределения чистой текущей стоимости проекта
Случай 4. Непересекающиеся кумулятивные профили рисков альтернативных (взаимоисключающих) проектов.
При фиксированной вероятности отдача проекта В всегда выше, нежели у проекта А. Профиль рисков также говорит о том, что при фиксированной NPV вероятность, с которой та будет достигнута, начиная с некоторого уровня, будет выше для проекта В, чем для проекта А. Таким образом, мы подошли к первому правилу.
Правило 1. Если кумулятивные профили рисков двух альтернативных проектов не пересекаются ни в одной точке, тогда следует выбирать тот проект, чей профиль рисков расположен правее.
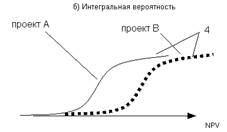
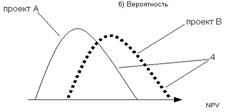
График непересекающихся кумулятивных профилей рисков альтернативных проектов
Случай 5. Пересекающиеся кумулятивные профили рисков альтернативных проектов.
Склонные к риску инвесторы предпочтут возможность получения высокой прибыли и, таким образом, выберут проект А. Несклонные к риску инвесторы предпочтут возможность нести низкие потери и, вероятно, выберут проект В.
Правило 2. Если кумулятивные профили риска альтернативных проектов пересекаются в какой-либо точке, то решение об инвестировании зависит от склонности к риску инвестора.
Ожидаемая стоимость агрегирует информацию, содержащуюся в вероятностном распределении. Она получается умножением каждого значения результативного показателя на соответствующую вероятность и последующего суммирования результатов. Сумма всех отрицательных значений показателя, перемноженных на соответствующие вероятности, есть ожидаемый убыток. Ожидаемый выигрыш – сумма всех положительных значений показателя, перемноженных на соответствующие вероятности. Ожидаемая стоимость есть, конечно, их сумма.
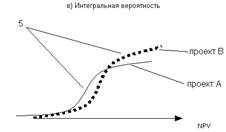
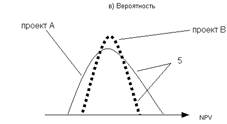
График пересекающихся кумулятивных профилей рисков альтернативных проектов
В качестве индикатора риска ожидаемая стоимость может выступать как надежная оценка только в ситуациях, где операция, связанная с данным риском, может быть повторена много раз. Хорошим примером такого риска служит риск, страхуемый страховыми компаниями, когда последние предлагают обычно одинаковые контракты большому числу клиентов. В инвестиционном проектировании мера ожидаемой стоимости должна всегда применяться в комбинации с такой мерой вариации, как стандартное отклонение.
Инвестиционное решение не должно базироваться лишь на одном значении ожидаемой стоимости, потому что индивид не может быть равнодушен к различным комбинациям значения показателя отдачи и соответствующей вероятности, из которых складывается ожидаемая стоимость.
Степень устойчивости проекта по отношению к возможным изменениям условий реализации, а значит, и степень риска, может быть охарактеризована показателями предельного уровня объемов производства, цен производимой продукции и других параметров проекта. Предельное значение параметра проекта для некоторого t-го года его реализации определяется как такое значение этого параметра в t-ом году, при котором чистая прибыль участника в этом году становится нулевой. Одним из наиболее важных показателей данного типа является точка безубыточности, характеризующая объем продаж, при котором выручка от реализации продукции совпадает с издержками производства. Для подтверждения работоспособности проектируемого производства необходимо, чтобы значение точки безубыточности было меньше значений номинальных объемов производства и продаж. Чем дальше от них значение точки безубыточности (в процентном отношении), тем устойчивее проект. Проект обычно признается устойчивым, если значение точки безубыточности не превышает 75% от номинального объема производства.
Как видно, данный показатель никак не связан с вероятностным методом и в отличие от последнего не уточняет вероятности и спектр возможных значений для результативных показателей. Кроме того, каждый показатель предельного уровня характеризует степень устойчивости в зависимости лишь от конкретного параметра проекта (объем производства и т. д.), в то время как вероятностный подход проводит комплексный анализ риска при неопределенности одновременно всех интересуемых параметров проекта, т. е. в последнем случае учитывается синхронность их изменения.
На практике не имеет смысла считать большое количество показателей предельного уровня с надеждой определить риски, так как основная цель расчета такого, несомненно, важного показателя, как точка безубыточности, состоит в том, чтобы определить минимально допустимый уровень объема производства на прединвестиционной фазе, что необходимо при описании проекта и построении его идеи.
Несмотря на свои достоинства, метод Монте-Карло не применяется широко в бизнесе. Одна из главных причин этого – неопределенность функций плотности переменных, которые используются при подсчете потоков наличности.
Другая проблема, которая возникает при использовании метода Монте-Карло, состоит в том, что его применение не дает однозначного ответа на вопрос о том, следует ли реализовывать данный проект или следует отвергнуть его.
При завершении анализа, проведенного методом Монте-Карло, у эксперта есть значение ожидаемой чистой приведенной стоимости проекта и плотность распределения этой случайной величины. Однако наличие этих данных не обеспечивает аналитика информацией о том, действительно ли прибыльность проекта достаточно велика, чтобы компенсировать риск по проекту, оцененный стандартным отклонением и коэффициентом вариации.
