Задачу управления отличает особенность: возможность не одного, а множества различных решений. Это обусловлено наличием в указанных задачах множества способов организации какого-либо процесса, приводящих к достижению определенной цели. Тем не менее задачу управления можно ставить как задачу нахождения хотя бы одного из возможных способов достижения поставленной цели.
Но такая постановка вопроса обычно бывает недостаточной. Следует вести речь о множестве решений и выбирать то из них, которое с некоторой принятой точки зрения является наилучшим.
При рассмотрении вариантов решения можно наложить на них добавочные требования, степень выполнения которых будет служить основанием для выбора. Очевидно, что достижение цели требует определенных ресурсов, и для каждого варианта достижения целевых установок необходимы разные объемы этих ресурсов. Поэтому в большинстве случаев выбирают тот вариант, который обеспечивает достижение цели с наименьшими затратами. Иногда основанием для выбора управленческого варианта выступают ограничения, налагаемые на систему управления. Здесь необходимо решать задачи оптимизации, т. е. находить минимальное или максимальное значения выбранного критерия управления при наличии определенных ограничений.
Для более наглядного представления возможных ограничений вспомним о том, что управление предприятием осуществляется при наличии определенных ограничений спроса на рынке, на производственные мощности и технологические процессы и т. п. В общем случае можно при управлении предприятием выделить два вида ограничений:
- законы и условия природы и другой внешней среды, в которой осуществляется управление;
- ограниченность ресурсов, используемых при управлении, которые в силу особенностей той или иной системы не могут или не должны превосходить некоторых пределов.
При математической формулировке задачи управления эти ограничения представляются обычно алгебраическими, дифференциальными или разностными уравнениями или неравенствами, связывающими переменные, описывающие состояние системы. Задачу управления можно считать сформулированной математически, если:
- сформулирована цель управления, выраженная через критерий управления;
- определены ограничения первого вида, представляющие собой системы дифференциальных или разностных уравнений, определяющих возможные способы развития системы;
- определены ограничения второго вида, представляющие собой систему алгебраических уравнений или неравенств, выражающих ограниченность ресурсов или иных величин, используемых при управлении.
Управление, которое удовлетворяет всем поставленным ограничениям и обращает в минимум (максимум) критерий управления, называют обычно оптимальным управлением. Линейное программирование является составной частью теории оптимизации, изучающей методы нахождения условного экстремума функций многих переменных.
Наличие компьютерной техники и программного обеспечения создали в настоящее время реальные предпосылки широкого использования метода линейного программирования для целей исследования СУ и принятия оптимальных управленческих решений. Данный метод достаточно глубоко проработан и широко проверен на практике при решении задач оптимального планирования.
С приемлемой точностью методом линейного программирования может решаться задача выбора оптимальной потребности в средствах. Его применение позволяет проводить расчеты по различным критериям оптимизации выбираемых типов оргтехники с соответствующими целевыми функциями. Наиболее целесообразными и необходимыми критериями оптимизации при решении такой задачи могут быть максимумы:
- выполняемой работы на рубль годовых приведенных затрат на единицу выполняемой работы;
- годовых приведенных затрат;
- производительности;
- единовременных затрат;
- занимаемой площади.
Рассмотрим задачу линейного программирования с ограничениями-равенствами – так называемую основную задачу линейного программирования. Основная задача линейного программирования ставится следующим образом.
Имеется ряд переменных: x1, x2, …, xn.
Требуется найти такие неотрицательные значения этих переменных, которые удовлетворяли бы системе линейных уравнений:
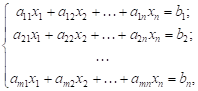
или в матричной форме:
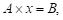
где

и, кроме того, обращали бы в минимум линейную функцию
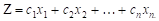
Очевидно, что случай, когда линейную функцию нужно обратить не в минимум, а в максимум, легко сводится к предыдущему, если изменить знак функции и рассмотреть вместо нее функцию:
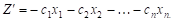
Условимся называть допустимым решением основной задачи любую совокупность переменных
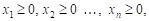
удовлетворяющую уравнениям.
Оптимальным решением будем называть то из допустимых решений, при котором линейная функция обращается в минимум.
Основная задача линейного программирования не обязательно должна иметь решение. Может оказаться, что уравнения противоречат друг другу или они имеют решения, но не в области неотрицательных значений x1, x2, …, xn. Тогда основная задача не имеет допустимых решений. Наконец, может оказаться, что допустимые решения основной задачи существуют, но среди них нет оптимального: функция Z в области допустимых решений не ограничена снизу.
Рассмотрим, прежде всего, вопрос о существовании допустимых решений основной задачи.
При решении этого вопроса необходимо исключить из рассмотрения линейную функцию Z, которую требуется минимизировать – наличие допустимых решений определяется только уравнениями.
Итак, пусть имеется система уравнений. Существуют ли неотрицательные значения x1, x2, …, xn, удовлетворяющие этой системе? Этот вопрос рассматривается в одном из разделов математики – линейной алгебре.
Приведем вкратце некоторые положения линейной алгебры, не останавливаясь на доказательствах соответствующих теорем.
Матрицей системы линейных уравнений является формула. Решенной матрицей системы линейных уравнений называется та же матрица, дополненная столбцом свободных членов:
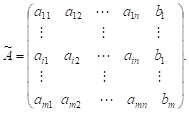
Рангом матрицы называется наибольший порядок отличного от нуля определителя, который можно получить, вычеркивая из матрицы какие-то строки и какие-то столбцы.
В линейной алгебре доказывается, что для совместимости системы линейных уравнений необходимо и достаточно, чтобы ранг матрицы системы был равен рангу ее расширенной матрицы.
Итак, если система уравнений-ограничений основной задачи совместна, то матрица системы и ее расширенная матрица имеют один и тот же ранг. Этот общий ранг r называется рангом системы, он представляет собой не что иное, как число линейно независимых уравнений среди наложенных ограничений.
Очевидно, ранг системы r не может быть больше числа уравнений m: r ≤ m.
Очевидно также, что ранг системы не может быть больше общего числа переменных: r ≤ n;
Действительно, ранг матрицы системы определяется как наибольший порядок определителя, составленного из элементов матрицы; так как число ее строк равно m, то r ≤ m; так как число ее столбцов равно n, то r ≤ n;
Структура задачи линейного программирования существенно зависит от ранга системы ограничений.
Рассмотрим, прежде всего, случай, когда r = n, т. е. когда число линейно независимых уравнений, входящих в систему, равно числу переменных n. Если отбросить избыточные уравнения, являющиеся линейными комбинациями других, то система уравнений-ограничений основной задачи принимает вид (т. е. m = n):
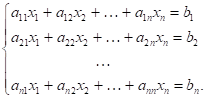
Так как r = n, то определитель, составленный из коэффициентов
 ,
,
не равен нулю. Из алгебры известно, что в этом случае система имеет единственное решение. Чтобы найти компоненту решения достаточно в определителе ∆ заменить i-й столбец столбцом xi свободных членов и полученный результат разделить на ∆.
Итак при r = n система уравнений-ограничений основной задачи имеет единственное решение: x1, x2, …, xn. Если в этом решении хотя бы одна величина x1, x2, …, xn отрицательна, это значит, что полученное решение недопустимо и основная задача не имеет решения.
Если все величины x1, x2, …, xn неотрицательны, то найденное решение является допустимым. Оно же является и оптимальным, поскольку единственно.
Очевидно, этот случай тривиален. Поэтому в дальнейшем будем рассматривать только случаи, когда r < n, т. е. когда число независимых уравнений, которым должны удовлетворять переменные x1, x2, …, xn меньше числа самих переменных. Тогда, если система совместна, у нее существует бесчисленное множество решений. При этом n–r переменным мы можем придавать произвольные значения (так называемые свободные переменные), а остальные r переменных выразятся через них (эти r переменных называют базисными).
Пример. Рассматривается система двух уравнений с четырьмя неизвестными:
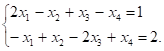
Ранг этой системы r = 2 (уравнения линейно независимы). Выберем в качестве свободных переменных, например, x3 и x4, а в качестве базисных – x1 и x2. Выразим базисные переменные через свободные. Имеем из уравнения:
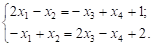
Складывая эти уравнения, получаем x1 = 3 + x3.
Умножая второе уравнение на 2 и складывая с первым, получаем: x2 = 3x3 – x4 + 5.
Таким образом, базисные переменные (x1, x2) выражены через свободные (x3, x4) Свободным переменным можно придавать любые значения, при этом будем всегда получать совокупность значений x1, x2, x3, x4, удовлетворяющую системе уравнений. Например, полагая x3 = x4 = 0, получаем x1 = 3, x2 = 5, и эти значения удовлетворяют системе.
Вообще, если ранг системы уравнений основной задачи (т. е. число линейно независимых уравнений, входящих в систему ограничений) равен r, то всегда можно выразить какие-то r базисных переменных через n–r остальных (свободных) и, придавая свободным переменным любые значения, получить бесчисленное множество решений системы.
В дальнейшем для простоты, записывая уравнения основной задачи, будем считать их линейно независимыми, при этом ранг системы r будет равен числу уравнений m.
Итак, если число уравнений основной задачи r = m меньше, чем число переменных n, то система линейных уравнений имеет бесчисленное множество решений, т. е. совокупностей значений x1, x2, …, xn, удовлетворяющих уравнениям-ограничениям. Если среди этих решений нет ни одного, для которого все x1, x2, …, xn неотрицательны, то это значит, что основная задача не имеет допустимого решения.
Если же существуют какие-то решения системы, для которых все x1, x2, …, xn неотрицательны, то каждое из них допустимо. Возникает задача – найти среди допустимых решений оптимальное, т. е. такое решение, для которого линейная функция Z = c1x1 + c2x2 + … + cnxn. обращается в минимум.
